計算科学は大規模な計算を主要な手段とする科学研究の方法論である。計算科学はコンピュータの発展により科学研究において重要な位置を占めるようになった。では人類が、計算が自然理解に役立つと気づいたのはいつからであろうか。

HPCwire Japan誌 のご厚意により、2014年から2020年にわたって、1964年以来のHPC (High Performance Computing) の歩みを『HPCの歩み50年』のタイトルで連載させていただきました。ご愛読を感謝いたします。最初はスタイルも定まらず、「海図のない航海」を始めたわけですが、書き進むうちにどうにかスタイルを確立することができました。またその間、新しい資料の発見があり、また1964年以前の動きも重要であることを痛感し、この度、新たに『新HPCの歩み』を連載させていただくことになりました。前のシリーズより、カバーする話題を広げました。

なお、本シリーズ執筆に際し、山田昭彦氏（元国立科学博物館）および前山和喜氏（総合研究大学院大学）から、貴重な助言や資料をいただきました。ここに感謝の意を表します。

科学における計算の歴史

計算科学(computational science)は大規模な計算を主要な手段とする科学研究の方法論である。計算科学はコンピュータの発展により科学研究において重要な位置を占めるようになった。現在では、実験的研究においても理論的研究においてもコンピュータの利用は不可欠であるが、だからといって全ての研究が計算科学なのではなく、あくまで大規模計算を主要な道具とする方法論を計算科学と呼ぶ。

計算科学には、大別してシミュレーション科学とデータ科学の2つの潮流がある。シミュレーションとは、対象とする系を要素の集まりと考え、要素を支配するミクロな基礎方程式を数値的に解くことにより、系のマクロな振舞いを調べる研究方法を指す。計算科学として最初に発展したのはシミュレーション科学であった。従来の科学研究は、複雑な現象の中から単純な法則を発見することに重点が置かれてきたが、シミュレーションにより、逆に、単純な法則から複雑な現象が「説明」できるようになった。初期の計算科学はシミュレーション科学であった。

他方、現代社会では膨大なデータが蓄積されつつある。その背景には、コンピュータ技術の発展、インターネット技術の発展、ユビキタス・コンピューティングの発展、センサー技術の発展、とくにモバイル機器に搭載されたセンサー群の登場などがある。その膨大なデータ（しばしば「ビッグデータ」と呼ばれる）を蓄積し、そこから意味のある情報を抽出し、制御や意志決定に活用する手法をデータ科学という。シミュレーション科学を実験、理論に続く第三の科学と位置づけるのに対し、アメリカのコンピュータ科学者ジム・グレイ(James N. Gray)はデータ科学を第四の科学と呼んだ（2007年）。さる大先生は「データがあればモデルは要らない」と言われたが、筆者はこのような考え方に批判的である。4つの方法論は互いに補完しあって自然の探求に向かうべきであると考える。これら4つの方法論の関係を筆者の独断で以下の図にまとめる。「理論」から「データ科学」への線が点線となっているのは、ぴったりしたキーワードが思いつかないからである。

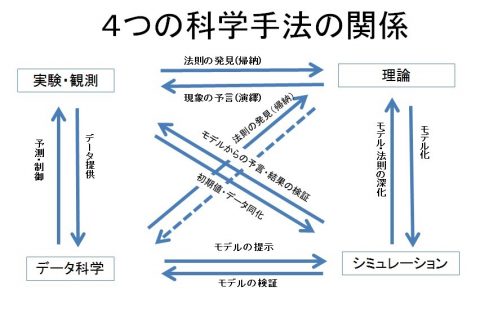では人類が、計算が自然理解に役立つと気づいたのはいつからであろうか。これはなかなかむつかしい問題である。筆者は科学史の専門家ではないが、科学史の本を紐解きながら考えた。（岩波講座計算科学第１巻『計算の科学』第4章参照）

1) 古代ギリシャ
古代ギリシャでは、自然に対し、それまでの神話的説明ではなく何かの根本原理に基づいて合理的な説明を試みる自然哲学(natural philosophy)と呼ばれる考察が行われた。例えばミレトス学派のタレース（BC 625～BC 547頃）は万物のアルケー（根源）は「水」であると考えたといわれる。「水」が何を意味していたかは分からないが、現代の観点から見ると、万物の根源を単純なものに求めるという発想は斬新である。タレースは、幾何学、測量、天文学にも通じていたと言われる。日食を予言した逸話は有名である。同じくミレトス学派のアナクジマンドロス（BC 610頃～BC 546）は万物のアルケーは「無限なるもの（ト・アペイロン）」であると論じた。その弟子アナクシメネス（BC 585～BC 525）は、万物のアルケーは「空気（プネウマ）」だと考えた。これらは自然科学のはるかな先駆と言えよう。

これに対しピタゴラス（BC 582頃～BC 496頃）は、万物のアルケーは「数」であり、日常生活から宇宙全体まで数が支配していると考え、数の性質を研究することにより、宇宙の真理を追究しようとした。一見自然に数量を導入したように見えるが、現象を定量的に記述するという考えはなく、現在の数の概念とはかなり発想が違うようである。また有理数と無理数の間に断絶を見るなど数に質の違いを主張した。

プラトン（BC 427頃～BC 347頃）は、ピタゴラス派と交流があり、数学・幾何学を重視した。数学は感覚を越えた真実在としてのイデアの概念を支える根拠になった。アリストテレス（BC 384～BC 322）は、その師プラトンとは異なり、経験を重視し、多くの自然現象とくに生物を並々ならぬ熱意をもって観察し優れた記録を残した。しかしかれは自然現象を生物の誕生・成長をモデルとして理解し、変化を終局の状態への移行と捉えた。かれの関心は始めと終わりの状態であって、途中の移行の過程を因果的に追求することは関心の外にあった。その結果、アリストテレスは経験を重視した反面、自然学から数学を閉め出すことになった。地上の物事は不完全であって、イデアの世界である数学で取り扱うことはできないと主張した（出典不明）。

したがって、古代ギリシャではさまざまな試みはあるものの、数学や計算が自然理解に役立つとは明確に考えていなかったようである。

2)イスラーム科学
ギリシャの諸知識はイスラーム世界でさらに発展した。「アルゴリズム」という語の語源となったという9世紀前半にアッバース朝時代のバグダードで活躍したアル・フワーリズミー(al-Khuwārizmī)（生年780または800、没年845または850）は、インドで発達した計算術や代数学を受け入れ、四則演算、代数方程式、幾何学、三角法などを発展させた。またインドの天文学の知識を使って、太陽、月、惑星の運動や食などを計算する天文表を作ったと言われる。当時としては大規模な計算を行ったものと思われる。かれは著書『代数学』（Hisab al-jabr w’al-muqabala）の冒頭で、「人間が必要としている計算というものを考察した後、私はこのすべてが数によることを見いだした。」（英訳：”When I considered what people generally want in calculating, I found that it always is a number.”）と書いている。ちなみに、algebra(代数学)という語はこの本の書名の一部al‐jabr(移項して負の項をなくす操作)に由来する。この書ではまだ負数や0は使われていない。また、イブン・アル・ハイサム(Ibn al-Haitham, 965-1040)は実験を重んじ、レンズや鏡をつかって光学などの実験的研究を行った。

ヨーロッパでは12世紀ごろ古代ギリシャやイスラーム世界の知識がアラビア語を経由して導入され、新しい学問体系が構築された。例えばイギリスの哲学者・修道士ロジャー・ベーコン(Roger Bacon, 1219頃-1292頃)はイブン・アル・ハイサムなどイスラーム科学の著作を読み、これに触発された実験や観察の重要性を説いた点は先駆的とされる。他方、占星術や錬金術にも強い関心を抱いていた。かれは、自然研究における数学の重要性を強調している。

自然研究における数学や計算の重要性を認識し始めたのは、どうもこのあたりにあるように思われる。

3) コペルニクス
16世紀になると、数量的な解析が科学上の成果を生むようになった。ポーランド出身の天文学者・司祭であったニコラウス・コペルニクス(Nicolaus Copernicus, 1473-1543)の主著“De Reolutionibus Orbium Coelestium”『天球の回転について』（全6巻）は亡くなる年に出版され地動説を主張した。地動説が書かれているのは第1巻の前半だけで、残りの大部分では三角法、球面天文学などの複雑な天文学計算手法による、太陽、月、惑星の天球上の見かけの運動の求め方について詳述している。かれの太陽中心説の背景には、古代ギリシャの太陽中心説とは異なり、高度に数学的、数量的な解析があったのである。

4) ケプラー
これをさらに精密化したのがドイツの天文学者ヨハネス・ケプラー(Johannes Kepler, 1571-1630)である。デンマークの天体観測者・占星術師のティコ・ブラーエ(Tycho Brahe, 1546-1601)はプラハ（現チェコ）に招聘されて天文台を造り、望遠鏡を使わず肉眼で観測し、膨大なデータを蓄積した。これにより占星術の精度を向上させようと考えたようである。ケプラーはこの膨大なデータを用いて、いわゆるケプラーの3法則を導いた。第1法則と第2法則は『新天文学、あるいは天体の自然学』（1609）（原書名“Astronomia Nova ΑΙΤΙΟΛΟΓΗΤΟΣ seu physica coelestis, tradita commentariis de motibus stellae Martis ex observationibus G.V. Tychonis Brahe”）において、第3法則は“Harmonices Mundi”『宇宙の調和について』(1619)で公表した。始めコペルニクスの円軌道で計算するとブラーエの観測値とわずか角度8分（1.16 m radian）のずれが生じたが、これを無視せず追求して楕円軌道のアイデアに達したという。精密科学である。

15世紀の神学者Nicolaus Cusanus（ニコラウス・クザーヌス、1401～1464）は、主著“De Docta Ignorantia”（『知ある無知』、1440）において、地球は他の星と同様であり、宇宙の中心ではなく、静止してもいないこと、天体は厳密な球形でなく、円軌道を描いていないことなど主張しており先駆的であるが、彼は観測によってではなく、形而上学的な思弁によりこのような主張に至った（薗田坦『クザーヌスの宇宙論の基礎』参照）。実際、コペルニクスやケプラーがクザーヌスのこの主張を知っていたかどうか、また知っていたとして彼らのパラダイムシフトにどのような影響を与えたのかについてはよく知らない。

5) ガリレオ
イタリアの物理学者・天文学者であるガリレオ・ガリレイ(Galileo Galilei, 1564-1642)は、望遠鏡を自ら製作して天体観測を行い、月面の凹凸、木星の4衛星、太陽黒点、金星の満ち欠けなどを発見し『星界の報告』(1610)に発表した。異端審問所の第一次裁判(1616)の後、彗星が月より下の現象であることを論証するために“Il Saggiatore”『贋金鑑識官』(1623)を出版した。彗星が月より下という話は間違いであったが、この本の中でこう述べている。「それ（宇宙という偉大な書物）は数学という言語で書かれている。数学を学ぶことなしに（この書物の）一語さえ理解することはできない。」（“Egli è scritto in lingua matematica, … senza i quali mezi è impossibile a intenderne umanamente parola”）かれの主張した数学的な科学方法論は、非常に革新的であった。

6) フランシス・ベーコン
イギリスの哲学者フランシス・ベーコン(Francis Bacon, 1561-1626)は、「知識は力なり」の名言で知られているが、自然現象への関心を鼓舞し、新しい方法論を提案した。主著“Novum Organum”『ノウム・オルガヌム（新しい道具）』(1620)では、収集した経験的事実から一般的な法則を導く帰納的な方法を示した。かれはガリレオの落体実験をいち早く取り上げ、「自然の探求は数学で終わるとき最良のものとなる」と述べている。

7) デカルト
経験を重視したベーコンと対照的に、フランスの自然哲学者ルネ・デカルト（René Descartes, 1596-1650）は自然現象と数学との一致に関心を持ち演繹的な方法を提案した。1618年頃オランダのブレダにおいて自然学を数学的手段で展開することを構想した。慣性の法則、運動量保存の法則、衝突の法則など基本的な法則を見いだし、「自然法則」という概念を確立した。デカルトは、自然は要素の組み合わせであり、自然現象はいくつかの原理から演繹的に説明されうるものと考えた。この方法の上に立って、1629年から数年、最初の機械論的宇宙論の体系といわれる『世界論－光に関する論考』を草した。この本の刊行は断念したが、1637年には“Discours de la méthode” 『方法序説』をライデンで公刊し、かれの主張する方法論を示した。

8) ライプニッツ
ドイツの学者ゴットフリート・ライプニッツ（Gottfried Wilhelm Leibniz, 1646-1716）は、微積分学を構築し、掛け算可能な歯車式機械計算器を製作したことでも知られている。かれは歯車式計算器により「天文学者たちを複雑な計算のために費やす時間と忍耐力から救う」ことを意図していた。天文学は多くの複雑な計算を必要とし、当時の計算科学であった。つまり、かれは計算という仕事を、人間にだけ許された高級な精神活動とは考えず、学者の手を煩わすに値しない労働と考えたのである。一方、ライプニッツは独立でありながら相互に反映しあうモナドが、一つの調和的宇宙を構成するという形而上学を立てた。そして人間の思考を少数の概念の組み合わせに分解することにより「人間思想のアルファベット」で諸学を統一することを考えていた。かれは推論のための汎用言語を考え、論証を計算に還元しようとした。記号論理学の先駆と言えよう。

9) ニュートン――自然法則へ
イギリスのアイザック・ニュートン（Sir Isaac Newton, 1643-1727グレゴリオ暦）は力学、光学、解析学の研究を進めたが、“Philosophiæ Naturalis Principia Mathematica”『自然哲学の数学的諸原理（プリンキピア）』(1687)において運動の法則を数学的に論じ、天体の運動や万有引力の法則を述べている。この書によって、古典力学の基礎が築かれた。

このようにして、「自然法則」という概念が成立するに至った。自然は自律した存在であって、自然の現象は例外のない普遍的な法則に支配されているという概念である。このような概念があって初めて、自然法則を探求する科学という枠組みが成立する。

このような自然法則という概念はそれほど古いものではない。先に見た通り、ギリシャの哲学者も中世の神学者も自然が従う法則という考えはもっていなかった。ガリレオでさえ、さまざまな法則を発見しながらも、自覚的に自然法則という概念を主張していない。自然にははっきりとした法則が確立されていて、宇宙に存在する一切の事物はこれに従うという考えを提示したのはデカルトである。かれはすべてを包括する絶対的な理論体系を構築することを夢見ていた。しかしアプリオリな原理の上に体系を構築しようするデカルトの自然学はうまくいかず、それにかわってニュートンの力学が脚光を浴びることになった。

こうして成立した学問体系にはいくつかの特徴がある。一つは要素論である。つまり種々の複雑な現象の背後には単純な要素があり、それが組み合わさって複雑な現象を作り出しているという考え方である。二つ目は数量化である。すなわち要素は質的にはすべて同等であり、量の差によって多様な現象が生まれるという考え方である。三つ目は法則の数量性である。つまり現象を支配する法則が、量と量との間の数学的な関係として記述されるということである。ここから科学における計算の重要性が出てくる。

10) 社会科学における計算
同じころ、自然現象に限らず人間の様々な行動や社会における様々な現象を数量的にとらえようという動きがみられる。社会契約説で有名なイギリスの哲学者トマス・ホッブス(Thomas Hobbes, 1588-1679)は、“De Corpore”『物体論』(1655)のChapter 1 “COMPUTATION OR LOGIC”の初めの方で「考えるとは計算することである」(原文“Per ratiocinationem autem intelligo computationen.”英訳“By ratiocination, I mean computation.”)と述べている。文脈はよく理解できないが、「計算」を自覚的に主張しているところが面白い。この著書の中で、円と同面積の正方形を求める方法（もちろん間違い）を主張して、大論争になった。

政治経済学の分野では、労働価値説を初めて唱えたイギリスの学者ウィリアム・ペティ(Sir William Petty, 1623-1687)は“Political Arithmetic posthum”『政治算術』(1690刊行、執筆は1670年代)において、「単に比較級や最上級の言葉を使いたり思弁的な議論をする代わりに、私の言おうとするところを数量numberと重量weightと尺度measureとによって表現する」と述べていることは注目される。現代流に言えば、定性的にではなく定量的に議論するということであろう。

ニュートンもある本（学生のノートとも言われている）の余白にラテン語で「“Numero pondere et mensura Deus omnia condidit.”（神は数と重さと尺度からすべてを創造した）」と自筆で記している。もっとも「数量と重量と尺度（長さ）」という表現は、旧約聖書続編『知恵の書』の「あなた（神）は、物差しと数と秤によって、すべてを桉配された。」(11:20聖書協会共同訳)からの引用と思われ、聖書の言葉を引用して数量的取り扱いの重要性を主張しているところはおもしろい。

フランスの医師、経済学者のフランソワ・ケネー(François Quesnay, 1694-1774)は、“Tableau économique”『経済表』(1758)を考案し、一国の経済循環の総体を数学的に表現しようとした。この考えの背景にはイギリスの解剖学者ウィリアム・ハーヴィ(William Harvey, 1578-1657)によって1628年に提唱された血液の体系的循環の思想があると言われる。この血液循環論はデカルトにも影響を与えている。

最近、社会科学や経済学でもスーパーコンピュータが利用され始めているが、その源泉は意外に古い。

11) ラプラス
計算が自然を決定するとまで述べたのはフランスのピエール-シモン・ラプラス(Pierre-Simon Laplace, 1749-1827)である。かれは“Théorie analytique des probabilités”『確率の解析的理論』(1812)の序論（後に“Essai philosophique sur les probabilités”『確率に関する哲学的試論』(1814)として出版）においてこのように述べた。「自然を動かしているすべての力と、それを構成するすべての存在のそれぞれの状況を知ることができる知的存在(une intelligence)が、もしこれらのデータを解析するに十分に大きな能力をもつならば、宇宙の最も巨大な物体から、最も軽い原子にいたるまでの運動を、同一の数式のなかに捉えることができるであろう。このような知性にとって不確定なものは何もなく、未来も過去と同様に眼前に現存するであろう。」

すなわち、宇宙のすべての原子の速度および位置がわかるならば、未来は完全に予測できると主張した。後に「ラプラスのデモン」と呼ばれるようになった古典論的決定論の主張である。今から考えるとシミュレーションまであと一歩に見えるが、当時はまだそのような計算能力には現実性がなかった。

12) 古典物理学の成立
ニュートンやライプニッツ等によって基礎づけられた数学的手法は、多くの学者の努力により18世紀に大きく発展した。運動への数学的分析の応用は古典力学として発展し、天体の運動に適用されただけでなく、ニュートンの物理学の方法論をあらゆる知的領域に広げようという努力がなされた。

ニュートンの物理学を貫くのは数学的方法であり、地上の現象から天体の運動まで統一的な説明に成功したことは数学的方法の勝利であった。18世紀にはニュートンの業績を数学的に整備することが多くの学者によってなされた。とくに、フランスのジャン・ル・ロン・ダランベール(Jean Le Rond d’Alembert, 1717-1783)やイタリア出身のジョゼフ-ルイ・ラグランジュ(Joseph-Louis Lagrange, 1736-1813)はニュートン力学を抽象化し解析力学を成立させた。他方、フランス百科全書派のドゥニ・ディドロ(Denis Diderot, 1713-1784)などは数学的方法の限界を主張し、帰納的方法の意義を強調した。

この頃、航海術からの要請もあり天文の測定精度が高まった。膨大な測定データが蓄積され、このようなデータを処理するために天体力学が大きく発展した。とくに太陽系の運動だけではなく、太陽系の生成と進化が問題となった。ラプラスは摂動法によって3体問題を解析し、2体問題として計算した結果と観測とのずれを、第3の惑星からの引力の影響（摂動）によって説明することに成功した。これにより、ニュートン力学の普遍性が示され、太陽系の安定性も証明された。

13) 産業革命へ
18世紀後半にイギリスで始まった産業革命は、科学と技術への新たな関心をもたらした。技術が科学と結びつき、教育と研究を推進するための公的な制度と機関が出現し、大きな役割を果たすようになった。「科学者 scientist」という言葉が生まれたのもこの頃である。現象をまず量的に測定しうる量によって記述し、その量の間の関係や時間的変化を数学的な式で表し、法則をつくる。得られた一般的な法則から、数学的解析により新しい現象を予言する、といいう物理学の方法論が次第に自覚されるようになった。電磁気、原子、熱、光などさまざまな分野が発展した。

数学的に定式化された物理法則を数値的に解くことについては、たとえばジョゼフ・フーリエ(Jean Baptiste Joseph Fourier, 1768-1830)がその重要性を強調している。フーリエは、1807年に熱伝導に関する最初の論文を提出したが、『熱の解析的理論』(1822)において、「熱伝導の微分方程式の解を数値的な利用が可能になるような形で解かなければ、この微分方程式を解いたことにならない」と強く主張している。かれはこのためフーリエ級数を考案した。振動や波動の解析は最初の目的ではなかった。

次回は機械式計算器について紹介する。